|
Αστρονομία
Το Ηλιακό Μας Σύστημα
| Ήλιος | Ερμής | Αφροδίτη | Γη | Σελήνη | Αρης | Ζ. Αστερ. | Δίας | Κρόνος | Ουρανός | Ποσειδώνας | Πλούτωνας |
 |  |  |  |  |  |  |  |  |  |  |  |
| |
 |
| Συγκριτικά μεγέθη των Πλανητών του Πλανητικού μας συστήματος |
ΤΡΟΧΙΑ ΠΛΑΝΗΤΩΝ
Λέγοντας τροχιά ενός ουράνιου σώματος εννοούμε το μονοπάτι που χαράσσει με την κίνησή του. Ως ουράνιο σώμα εννοούμε είτε κάποιον πλανήτη νάνο ή μη, είτε κάποιον κομήτη. Τα ουράνια αυτά σώματα εκτελούν χαρακτηριστικές κινήσεις γύρω από κάποιο αστέρι. Οι κινήσεις αυτές συνήθως δεν είναι ακριβώς κυκλικές αλλά έχουν την μορφή έλλειψης ή παραβολής ή υπερβολής. Οι πλανήτες σε ένα πλανητικό σύστημα, διαγράφουν ελλειπτική τροχιά, στην μία εστία της οποίας βρίσκεται το αστέρι. Σε περίπτωση που το πλανητικό σύστημα έχει δύο αστέρια, τότε οι πλανήτες κινούνται ελλειπτικά γύρω από το κέντρο βάρος τους. Στο δικό μας πλανητικό σύστημα, ο Ήλιος είναι το μοναδικό αστέρι γύρω από το οποίο περιστρέφονται οι πλανήτες σε ελλειπτικές τροχιές με την μία εστία της έλλειψης να καταλαμβάνεται από τον Ήλιο.
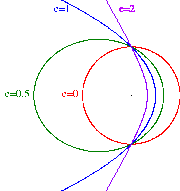
Η σημαντικότερη παράμετρος που περιγράφει την τροχιά των ουράνιων σωμάτων είναι η εκκεντρότητα. Η εκκεντρότητα είναι το μέγεθος που χαρακτηρίζει κάθε κωνική τομή (λέγοντας κωνική τομή εννοούμε το σχήμα που μπορεί να προκύψει από την τομή ενός κώνου με ένα επίπεδο). Την συμβολίζουμε με το e, και μπορεί να πάρει τιμές από 0 έως άπειρο. Ειδικότερα:
Σε ένα κύκλο είναι 0,
Σε μία έλλειψη είναι μεγαλύτερη του μηδενός και μικρότερη της μονάδας,
Σε μία παραβολή είναι ίση με 1,
Σε μία υπερβολή είναι μεγαλύτερη της μονάς όχι όμως άπειρη και τέλος
Σε μία ευθεία είναι ή 1 ή άπειρο ανάλογα με ον ορισμό.
Από τα παραπάνω γίνεται φανερό ότι η καμπυλότητα της τροχιάς μειώνεται με την αύξηση της εκκεντρότητας, όπως φαίνεται και στο σχήμα παρακάτω
Ο μαθηματικός τύπος της εκκεντρότητας είναι: e=sqtr(1-k(b*b/a*a)),
Sqrt , η τετραγωνική ρίζα,
k , ίσο με +1 για την έλλειψη, 0 για την παραβολή και -1 για την υπερβολή.
b, το μήκος του μικρός ημιάξονα
a, το μήκος του μεγάλου ημιάξονα.
Για την ελλειπτική τροχιά που διαγράφουν οι πλανήτες στο πλανητικό μας σύστημα ο τύπος της εκκεντρότητας γίνεται: e=sqtr(1 - b*b/a*a)και όπως είπαμε και παραπάνω μπορεί να πάρει τιμές από 0 έως 1 ενώ όσο αυξάνεται η τιμή αυτή τόσο μειώνεται η καμπυλότητας, τόσο δηλαδή αποκλίνουμε από την κυκλική τροχιά. Στον παρακάτω πίνακα μπορούμε να δούμε συγκεντρωτικά της εκκεντρότητες των πλανητών του πλανητικού μας συστήματος.
| ΠΛΑΝΗΤΗΣ | ΕΚΚΕΝΤΡΟΤΗΤΑ |
| ΕΡΜΗΣ | 0,20563069 |
| ΑΦΡΟΔΙΤΗ | 0,00677323 |
| ΓΗ | 0,01671022 |
| ΑΡΗΣ | 0,09341233 |
| ΔΙΑΣ | 0,04839266 |
| ΚΡΟΝΟΣ | 0,05415060 |
| ΟΥΡΑΝΟΣ | 0,04716771 |
| ΠΟΣΕΙΔΩΝΑΣ | 0,00858587 |
| ΠΛΟΥΤΩΝΑΣ | 0,24880766 |
Όπως γίνεται φανερό από τον παραπάνω πίνακα, οι τροχιές της Αφροδίτης και του Ποσειδώνα έχουν την μικρότερη εκκεντρότητα, το οποίο σημαίνει ότι είναι πιο κοντά στην κυκλική τροχιά, ενώ αντίθετα οι τροχιά του Πλούτωνα και του Ερμή έχουν την μεγαλύτερη εκκεντρότητα και αποκλίνουν περισσότερο από την κυκλική από τους άλλους πλανήτες.
|
|